Do differing morphological techniques provide different results? What are some applications of landmark-based geometric morphometrics?

Shape is defined as the specific form of a distinct object that is invariant to changes in position, rotation and scale, and many methods have been proposed to study shape. For instance, sets of linear distances may be measured on each individual (e.g., length, width and height) to represent shape (Figure 5A), as well as angles (Figure 5B) and ratios of these measurements.

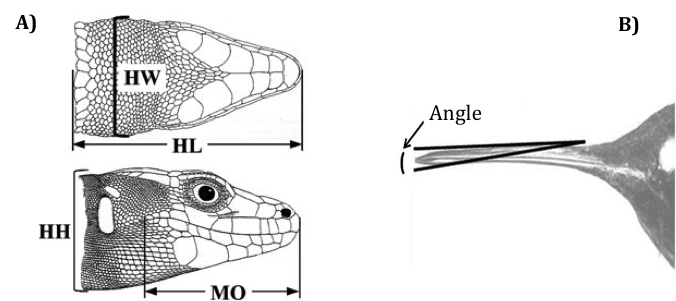
Figure 1. A) Sets of linear distances: Head length (HL), head width (HW), head height (HH), and mouth opening (MO) and B) Measurement of angle. A): adapted from Kaliontzopoulou et al. 2012. B): adapted from Berns and Adams, 2010

Sets of linear distances do not always accurately capture shape because of shortcomings that limit their general utility. For instance, it is possible that for some objects the same set of distance measurements may be obtained from two different shapes (see Fig. 2), because the location of the measurements is not recorded in the distance measures themselves. For example, if the maximum length and width were taken on an oval and teardrop, the linear values might be the same even though the shapes are clearly different (see Figure 3).

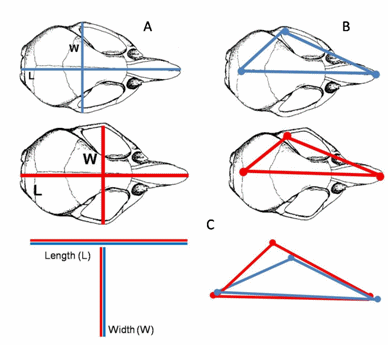
Fig. 2
A) Linear measurements capture a certain level of shape, however we can't observe complexity and therefore, we lose details. Here the width that crosses length has been shifted between the two skulls. These linear measurements reveal the same shape when the measurements are put side by side.
B) After placing landmarks on the skulls instead of linear distances, the differences in shape are now clear.
C) Linear measurements showing the same shape and landmarks showing true shape.

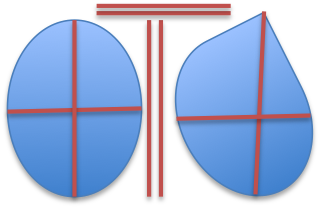
Fig. 3 Maximum height and width taken on two different shapes results in the same linear measurement on both

A major advance in the study of shape is landmark-based geometric morphometric methods, which do not have these difficulties. These methods quantify the shape of anatomical objects using the Cartesian coordinates biologically homologous landmarks whose location is identified on each specimen (Figure 4). These landmarks can be digitized in either two- or three-dimensions, and provide a means of shape quantification that enables graphical representations of shape (see below).

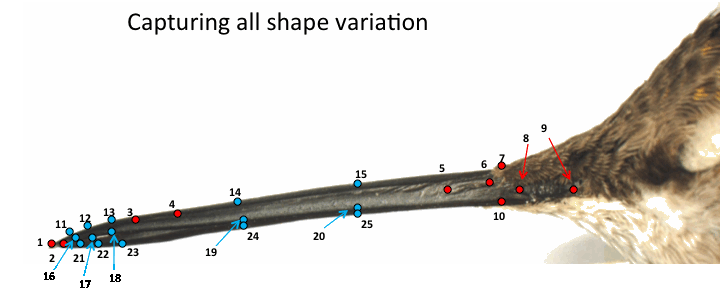
Fig. 4 Landmarks in images of hummingbird bills to capture shape variation. Red landmarks represent biologically homologous points, blue indicates semi-landmarks

Geometric morphometric analyses of shape are accomplished in several sequential steps. First, the landmark coordinates are digitized from each specimen. Next, differences in specimen position, orientation and size are eliminated through a generalized Procrustes analysis. This procedure translates all specimens to the origin, scales them to unit centroid size, and optimally rotates them to minimize the total sums-of-squares deviations of the landmark coordinates from all specimens to the average configuration (see Fig. 5). The resulting aligned Procrustes shape coordinates describe the location of each specimen in a curved space related to Kendall’s shape space. These are then projected orthogonally into a linear tangent space yielding Kendall’s tangent space coordinates, which can then be treated as a set of shape variables for further analyses of shape variation and covariation with other variables.

Fig. 5 Procedure for removing non-shape variation. A) Obtain raw data, B) Align to the centroid, C) Once aligned to a common point, rotate until object is on the same plane, and D) Scale so all objects are the same size. This leaves only shape variation.

Depending on the biological question at hand, sets of linear measurements and geometric morphometric methods can be appropriate and have been utilized to identify patterns of shape dimorphism in numerous taxa, including fish, turtles, birds and lizards, to name a few.

For further discussion, see:
Adams, D.C., Berns, C.M., Kozak, K.H. & Weins, J.J. Are rates of speciation correlated with rates of morphological evolution? Proceedings of the Royal Society of London Series B-Biological Sciences (2009)
Adams, D.C., Rohlf, F.J. & Slice, D.E. Geometric morphometrics: ten years of progress following the 'revolution'. Italian Journal of Zoology 71, 5-16 (2004)